
Μπορεί να έχετε ακούσει τον όρο «Markov αλυσίδα» πριν, αλλά αν δεν έχετε πάρει μερικές τάξεις σχετικά με την θεωρία πιθανοτήτων ή τους αλγορίθμους της επιστήμης της πληροφορικής Πώς να μάθετε τον προγραμματισμό χωρίς το άγχος Πώς να μάθετε τον προγραμματισμό χωρίς όλο το άγχος Ίσως έχετε αποφασίσει να να ακολουθήσετε προγραμματισμό, είτε για επαγγελματική σταδιοδρομία είτε ως χόμπι. Εξαιρετική! Αλλά ίσως αρχίζετε να αισθάνεστε συγκλονισμένοι. Οχι και τόσο καλό. Εδώ μπορείτε να διευκολύνετε το ταξίδι σας. Διαβάστε περισσότερα, πιθανώς δεν ξέρετε τι είναι, πώς λειτουργούν και γιατί είναι τόσο σημαντικό.
Η έννοια της αλυσίδας Markov είναι μια έννοια "κάτω από την κουκούλα", που σημαίνει ότι δεν χρειάζεται πραγματικά να γνωρίζετε τι είναι για να επωφεληθείτε από αυτές. Ωστόσο, μπορείτε σίγουρα να επωφεληθείτε από την κατανόηση του τρόπου λειτουργίας τους. Είναι απλά αλλά χρήσιμα με πολλούς τρόπους.
Έτσι, εδώ είναι μια διαδρομή συντριβής - όλα όσα πρέπει να ξέρετε για τις αλυσίδες Markov συμπυκνωμένο κάτω σε ένα μόνο, εύπεπτο άρθρο. Αν θέλετε να εμβαθύνετε ακόμα πιο βαθιά, δοκιμάστε το μάθημα της ελεύθερης θεωρίας πληροφοριών στην Ακαδημία Khan (και εξετάστε και άλλες ιστοσελίδες διαδικτυακού μαθήματος επίσης 8 τρομερές ιστοσελίδες για να πάρετε δωρεάν μαθήματα κολλεγίων σε απευθείας σύνδεση 8 τρομερές ιστοσελίδες για να λάβετε δωρεάν μαθήματα κολλεγίων online Διαβάστε περισσότερα).
Markov Αλυσίδες 101
Ας υποθέσουμε ότι θέλετε να προβλέψετε τι θα είναι ο καιρός αύριο. Μια πραγματική πρόβλεψη - το είδος που εκτελούνται από μετεωρολόγους εμπειρογνώμονα 7 Best Free Weather Apps για το Android 7 Best Free Weather Apps για Android Διαβάστε περισσότερα - θα περιλαμβάνει εκατοντάδες ή ακόμα και χιλιάδες διαφορετικές μεταβλητές που αλλάζουν συνεχώς. Τα συστήματα καιρού είναι απίστευτα περίπλοκα και αδύνατα να μοντελοποιηθούν, τουλάχιστον για λαϊκούς όπως εσείς και εγώ. Αλλά μπορούμε να απλοποιήσουμε το πρόβλημα χρησιμοποιώντας εκτιμήσεις πιθανότητας.
Φανταστείτε ότι είχατε πρόσβαση σε τριάντα χρόνια από τα καιρικά δεδομένα. Αρχίζετε στην αρχή, σημειώνοντας ότι η Ημέρα 1 ήταν ηλιόλουστη. Συνεχίζετε, σημειώνοντας ότι η Ημέρα 2 ήταν επίσης ηλιόλουστη, αλλά η Ημέρα 3 ήταν θολό, και η 4η ημέρα ήταν βροχερή, η οποία οδήγησε σε καταιγίδα την Ημέρα 5, ακολουθούμενη από ηλιόλουστες και σαφείς ουρανούς την Ημέρα 6.
Στην ιδανική περίπτωση θα ήταν πιο κοκκώδης, επιλέγοντας μια ανάλυση ανά ώρα ανά ώρα αντί για μια ανάλυση ημέρας, αλλά αυτό είναι μόνο ένα παράδειγμα για να απεικονίσει την έννοια, έτσι φέρτε μαζί μου!
Αυτό το κάνετε σε όλο το σύνολο δεδομένων των 30 ετών (το οποίο θα ήταν απλά ντροπαλό των 11.000 ημερών) και να υπολογίσετε τις πιθανότητες του καιρού του αύριο με βάση τον καιρό. Για παράδειγμα, εάν είναι σήμερα ηλιόλουστο, τότε:
- Μια πιθανότητα 50 τοις εκατό που αύριο θα είναι και πάλι ηλιόλουστη.
- Μια πιθανότητα 30 τοις εκατό που αύριο θα είναι συννεφιασμένη.
- Μια πιθανότητα 20 τοις εκατό που αύριο θα είναι βροχερή.
Τώρα επαναλάβετε αυτό για κάθε πιθανή καιρική κατάσταση. Εάν είναι σήμερα θολό, ποιες είναι οι πιθανότητες ότι το αύριο θα είναι ηλιόλουστο, βροχερό, ομίχλη, καταιγίδες, χαλαζοί, ανεμοστρόβιλοι κ.λπ .; Πολύ σύντομα, έχετε ένα ολόκληρο σύστημα πιθανοτήτων που μπορείτε να χρησιμοποιήσετε για να προβλέψετε όχι μόνο τον καιρό του αύριο, αλλά τον καιρό της επόμενης ημέρας και την επόμενη μέρα.
Μεταβατικά κράτη
Αυτή είναι η ουσία μιας αλυσίδας Markov. Έχετε μεμονωμένες καταστάσεις (σε αυτή την περίπτωση, καιρικές συνθήκες) όπου κάθε κράτος μπορεί να μεταβεί σε άλλες πολιτείες (π.χ. ηλιόλουστες μέρες μπορούν να μεταβαίνουν σε συννεφιασμένες ημέρες) και αυτές οι μεταβάσεις βασίζονται σε πιθανότητες. Εάν θέλετε να προβλέψετε τι μπορεί να είναι ο καιρός σε μια εβδομάδα, μπορείτε να εξερευνήσετε τις διάφορες πιθανότητες τις επόμενες επτά ημέρες και να δείτε ποιες είναι οι πιθανότερες. Έτσι, μια "αλυσίδα" Markov.
Ποιος είναι ο Μάρκοφ; Ήταν ένας Ρώσος μαθηματικός, ο οποίος κατέληξε σε μια ολόκληρη ιδέα ενός κράτους που οδηγούσε απευθείας σε άλλο κράτος με βάση μια ορισμένη πιθανότητα, όπου κανένας άλλος παράγοντας δεν επηρέασε τη μεταβατική ευκαιρία. Βασικά, εφευρέθηκε η αλυσίδα Markov, εξ ου και η ονομασία.
Πώς χρησιμοποιούνται αλυσίδες Markov στον πραγματικό κόσμο
Με την εξήγηση έξω από το δρόμο, ας εξερευνήσουμε κάποιες από τις εφαρμογές πραγματικού κόσμου όπου έρχονται σε πρακτικό. Ίσως να εκπλαγείτε να διαπιστώσετε ότι χρησιμοποιείτε τις αλυσίδες Markov όλη αυτή τη φορά χωρίς να το γνωρίζετε!
Δημιουργία ονόματος
Έχετε συμμετάσχει ποτέ σε επιτραπέζια παιχνίδια, παιχνίδια MMORPG ή ακόμα και σε φανταστικές εκδόσεις; Μπορεί να έχετε αγωνιστεί για την ονοματοδοσία των χαρακτήρων σας (τουλάχιστον σε ένα σημείο ή άλλο) - και όταν απλά δεν φαινόταν να σκέφτεστε ένα όνομα που σας αρέσει, πιθανόν να καταφύγετε σε μια γεννήτρια γενικών ονομασιών Δημιουργήστε ένα νέο ψευδώνυμο με το Best Generators Online Name [Παράξενο και θαυμαστό Web] Δημιουργήστε ένα νέο ψευδώνυμο με τις καλύτερες γεννήτριες γενικών ονομασιών [Weird & Wonderful Web] Το όνομά σας είναι βαρετό. Ευτυχώς, μπορείτε να μεταβείτε στο διαδίκτυο και να επιλέξετε ένα νέο ψευδώνυμο χρησιμοποιώντας μία από τις αμέτρητες γεννήτριες ονομασιών που είναι διαθέσιμες στο Internetz. Διαβάστε περισσότερα .
Έχετε αναρωτηθεί ποτέ πώς λειτούργησαν αυτές οι γεννήτριες; Όπως αποδεικνύεται, πολλοί από αυτούς χρησιμοποιούν Markov αλυσίδες, καθιστώντας την μία από τις πιο χρησιμοποιούμενες λύσεις. (Υπάρχουν άλλοι αλγόριθμοι εκεί έξω που είναι εξίσου αποτελεσματικοί, φυσικά!)
Το μόνο που χρειάζεστε είναι μια συλλογή γραμμάτων, όπου κάθε γράμμα έχει μια λίστα πιθανών επακόλουθων γραμμάτων με πιθανότητες. Έτσι, για παράδειγμα, το γράμμα "Μ" έχει 60% πιθανότητα να οδηγήσει στο γράμμα "Α" και 40% ευκαιρία να οδηγήσει στο γράμμα "εγώ". Κάνετε αυτό για μια ολόκληρη δέσμη άλλων γραμμάτων, στη συνέχεια εκτελέστε τον αλγόριθμο. Boom, έχετε ένα όνομα που έχει νόημα! (Τις περισσότερες φορές, ούτως ή άλλως.)
Google PageRank
Μια από τις ενδιαφέρουσες συνέπειες της θεωρίας της αλυσίδας Markov είναι ότι καθώς αυξάνεται το μήκος της αλυσίδας (δηλαδή αυξάνεται ο αριθμός των μεταβολών της κατάστασης), η πιθανότητα να προσγειωθείτε σε μια συγκεκριμένη κατάσταση συγκλίνει σε σταθερό αριθμό και αυτή η πιθανότητα είναι ανεξάρτητη από το πού ξεκινάτε στο σύστημα.
Αυτό είναι εξαιρετικά ενδιαφέρον όταν σκέφτεστε ολόκληρο τον παγκόσμιο ιστό ως σύστημα Markov όπου κάθε ιστοσελίδα είναι μια κατάσταση και οι δεσμοί μεταξύ των ιστοσελίδων είναι μεταβάσεις με πιθανότητες. Αυτό το θεώρημα βασικά λέει ότι ανεξάρτητα από το ποια ιστοσελίδα ξεκινάτε, η πιθανότητά σας να προσγειωθείτε σε μια συγκεκριμένη ιστοσελίδα Χ είναι μια σταθερή πιθανότητα, υποθέτοντας ένα "μεγάλο χρονικό διάστημα" σερφ .
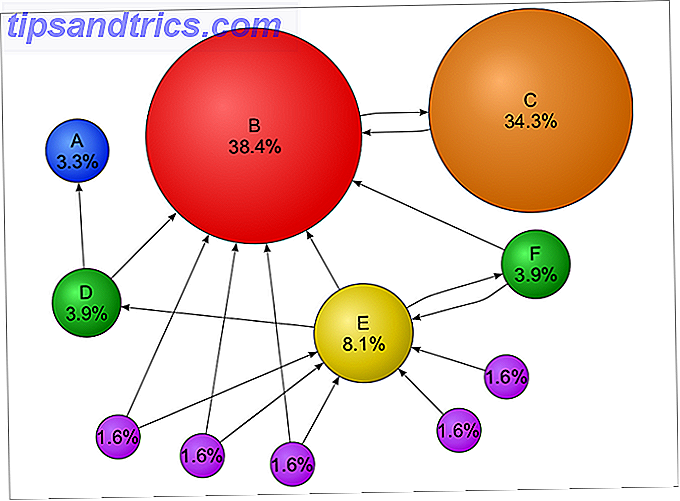
Και αυτή είναι η βάση για το πώς η Google κατατάσσει ιστοσελίδες. Πράγματι, ο αλγόριθμος PageRank είναι μια τροποποιημένη (ανάγνωση: πιο προηγμένη) μορφή του αλγορίθμου της αλυσίδας Markov.
Όσο υψηλότερη είναι η "σταθερή πιθανότητα" να φθάσει σε μια συγκεκριμένη ιστοσελίδα, τόσο υψηλότερη είναι η PageRank. Αυτό συμβαίνει επειδή μια υψηλότερη σταθερή πιθανότητα υποδηλώνει ότι η ιστοσελίδα έχει πολλές εισερχόμενες συνδέσεις από άλλες ιστοσελίδες - και η Google υποθέτει ότι εάν μια ιστοσελίδα έχει πολλές εισερχόμενες συνδέσεις, τότε πρέπει να είναι πολύτιμη. Όσο περισσότερες εισερχόμενες συνδέσεις, τόσο πιο πολύτιμες είναι.
Είναι πιο περίπλοκο από αυτό, φυσικά, αλλά έχει νόημα. Γιατί ένας ιστότοπος όπως το About.com έχει μεγαλύτερη προτεραιότητα στις σελίδες αποτελεσμάτων αναζήτησης; Επειδή αποδεικνύεται ότι οι χρήστες τείνουν να φθάνουν εκεί καθώς κινούνται στο διαδίκτυο. Ενδιαφέρουσες, έτσι δεν είναι;
Πληκτρολόγηση πρόβλεψης λέξεων
Τα κινητά τηλέφωνα είχαν προβλέψιμη πληκτρολόγηση για δεκαετίες τώρα, αλλά μπορείτε να μαντέψετε πώς γίνονται αυτές οι προβλέψεις; Είτε χρησιμοποιείτε το Android (εναλλακτικές επιλογές πληκτρολογίου Ποιο είναι το καλύτερο εναλλακτικό πληκτρολόγιο για το Android; Ποιο είναι το καλύτερο εναλλακτικό πληκτρολόγιο για Android; Περισσότερα) ή iOS (εναλλακτικές επιλογές πληκτρολογίου 9 Εναλλακτικά πληκτρολόγια iOS για να κάνετε τη δακτυλογράφηση σας πιο εύκολη ή πιο διασκεδαστική 9 Εναλλακτικά πληκτρολόγια iOS για να κάνετε δακτυλογράφηση σας πιο εύκολη ή πιο διασκεδαστική Όταν η Apple τελικά σταμάτησε να ενεργεί σαν υπερπροστατευτικός γονέας και εισήγαγε πληκτρολόγια τρίτων, πληκτρολογίου-τρελό. Διαβάστε περισσότερα), υπάρχει μια καλή πιθανότητα η εφαρμογή σας να χρησιμοποιεί αλυσίδες Markov.
Αυτός είναι ο λόγος για τον οποίο οι εφαρμογές πληκτρολογίου ρωτούν εάν μπορούν να συλλέξουν δεδομένα σχετικά με τις συνήθειες δακτυλογράφησης. Για παράδειγμα, στο Google Keyboard, υπάρχει μια ρύθμιση που ονομάζεται αποσπάσματα κοινής χρήσης που ζητά να "μοιράζονται αποσπάσματα από το τι και πώς πληκτρολογείτε στις εφαρμογές Google για να βελτιώσετε το πληκτρολόγιο Google". Στην ουσία, τα λόγια σας αναλύονται και ενσωματώνονται στις πιθανότητες αλυσίδας Markov της εφαρμογής.
Αυτός είναι και ο λόγος για τον οποίο οι εφαρμογές πληκτρολογίου παρουσιάζουν συχνά τρεις ή περισσότερες επιλογές, κατά κανόνα από τη σειρά των πιθανότερων σε λιγότερο πιθανές. Δεν μπορεί να ξέρει με σιγουριά τι εννοούσε να πληκτρολογήσετε στη συνέχεια, αλλά είναι σωστό πιο συχνά από ό, τι δεν είναι.
Προσομοίωση υποδέντρου
Εάν δεν έχετε χρησιμοποιήσει ποτέ το Reddit, σας συνιστούμε να δείτε τουλάχιστον αυτό το συναρπαστικό πείραμα που ονομάζεται / r / SubredditSimulator.
Με απλά λόγια, ο Subreddit Simulator παίρνει ένα τεράστιο κομμάτι από ΟΛΑ τα σχόλια και τους τίτλους που έγιναν στις πολυάριθμες κοινότητες του Reddit, και στη συνέχεια αναλύει τη λέξη για λέξη μακιγιάζ κάθε φράσης. Χρησιμοποιώντας αυτά τα δεδομένα, δημιουργεί πιθανότητες λέξης προς λέξη - τότε χρησιμοποιεί αυτές τις πιθανότητες για να δημιουργήσει τίτλους και σχόλια από το μηδέν.
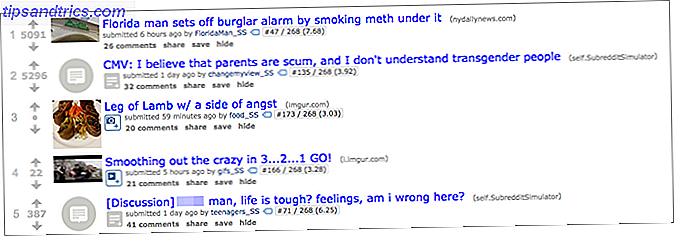
Ένα ενδιαφέρον στρώμα σε αυτό το πείραμα είναι ότι τα σχόλια και οι τίτλοι κατηγοριοποιούνται από την κοινότητα από την οποία προέρχονται τα δεδομένα, οπότε τα είδη σχολίων και τίτλων που δημιουργούνται από το σύνολο δεδομένων του / r / food είναι άγρια διαφορετικά από τα σχόλια και τους τίτλους που δημιουργεί το / r / σύνολο δεδομένων ποδοσφαίρου.
Και το πιο αστείο - ή ίσως το πιο ενοχλητικό - μέρος όλων αυτών είναι ότι τα παραγόμενα σχόλια και τίτλοι συχνά δεν μπορούν να διακριθούν από αυτά που δημιουργούνται από τους πραγματικούς ανθρώπους. Είναι απολύτως συναρπαστικό.
Ξέρετε για οποιεσδήποτε άλλες δροσερές χρήσεις για τις αλυσίδες Markov; Έχετε ερωτήσεις που χρειάζονται ακόμη απάντηση; Ενημερώστε μας σε ένα σχόλιο παρακάτω!



